Data and Methodology#
The project uses primarily input–output (IO) data and theory to calculate life cycle module results, complying with consequential life cycle assessment (LCA) concepts. Here we describe the methodology underlying BONSAI-IO and detailed information on the data included.
1. The Make-use Framework#
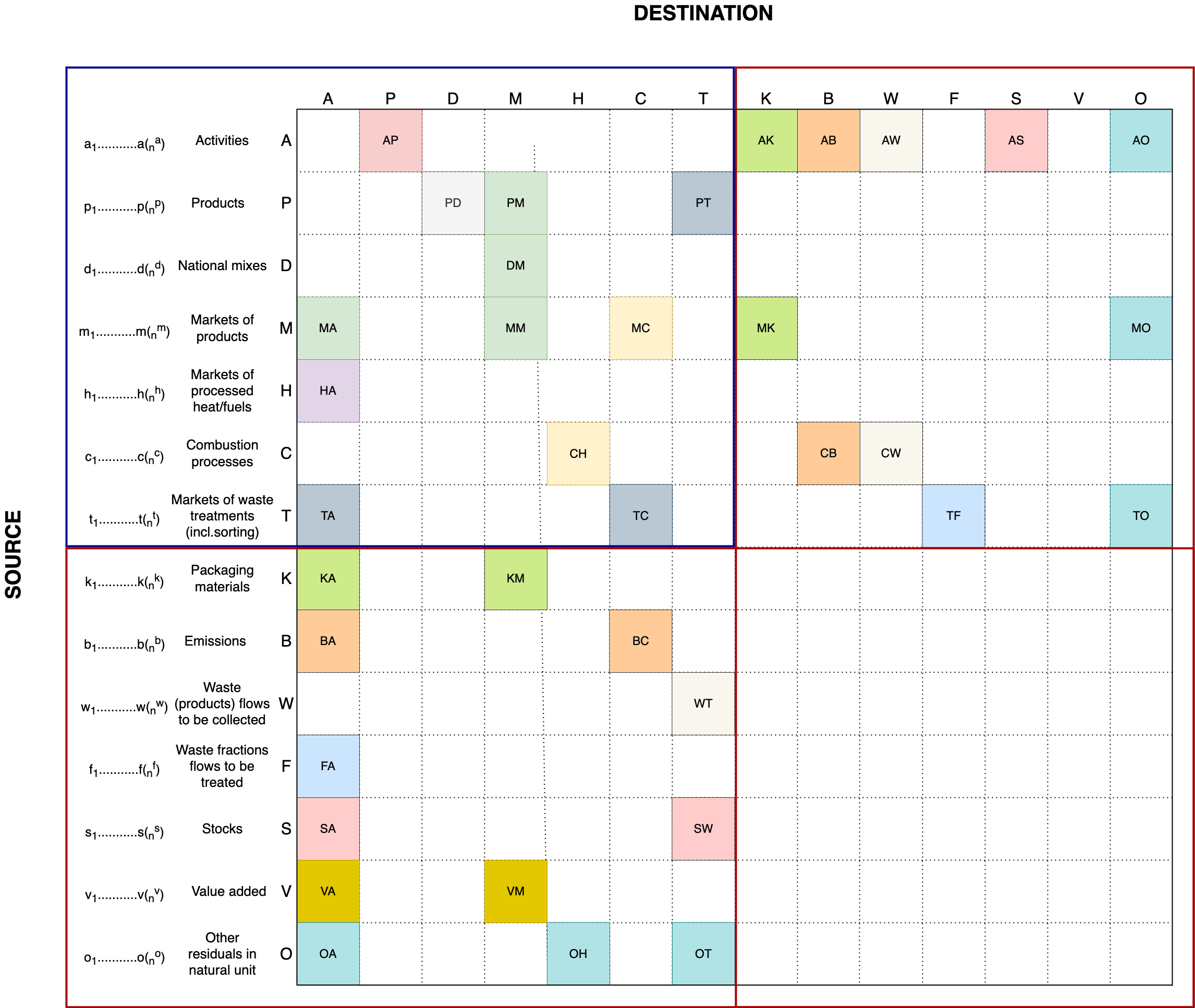
The following picture shows the structure of BONSAI IO following the the make-use framework (see the terminology in Glossary section):
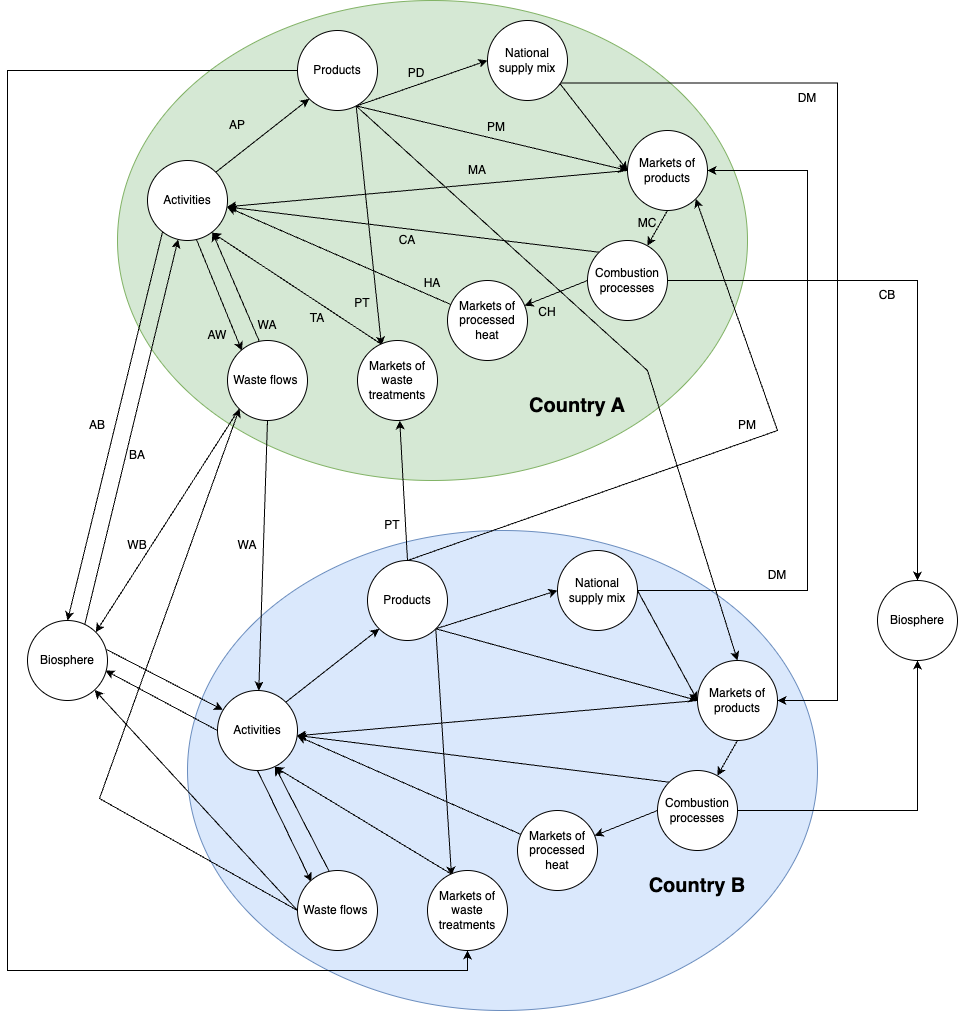
An alternative illustration:
Core Concepts#
Here we define some concepts that are essential in the BONSAI IO framework
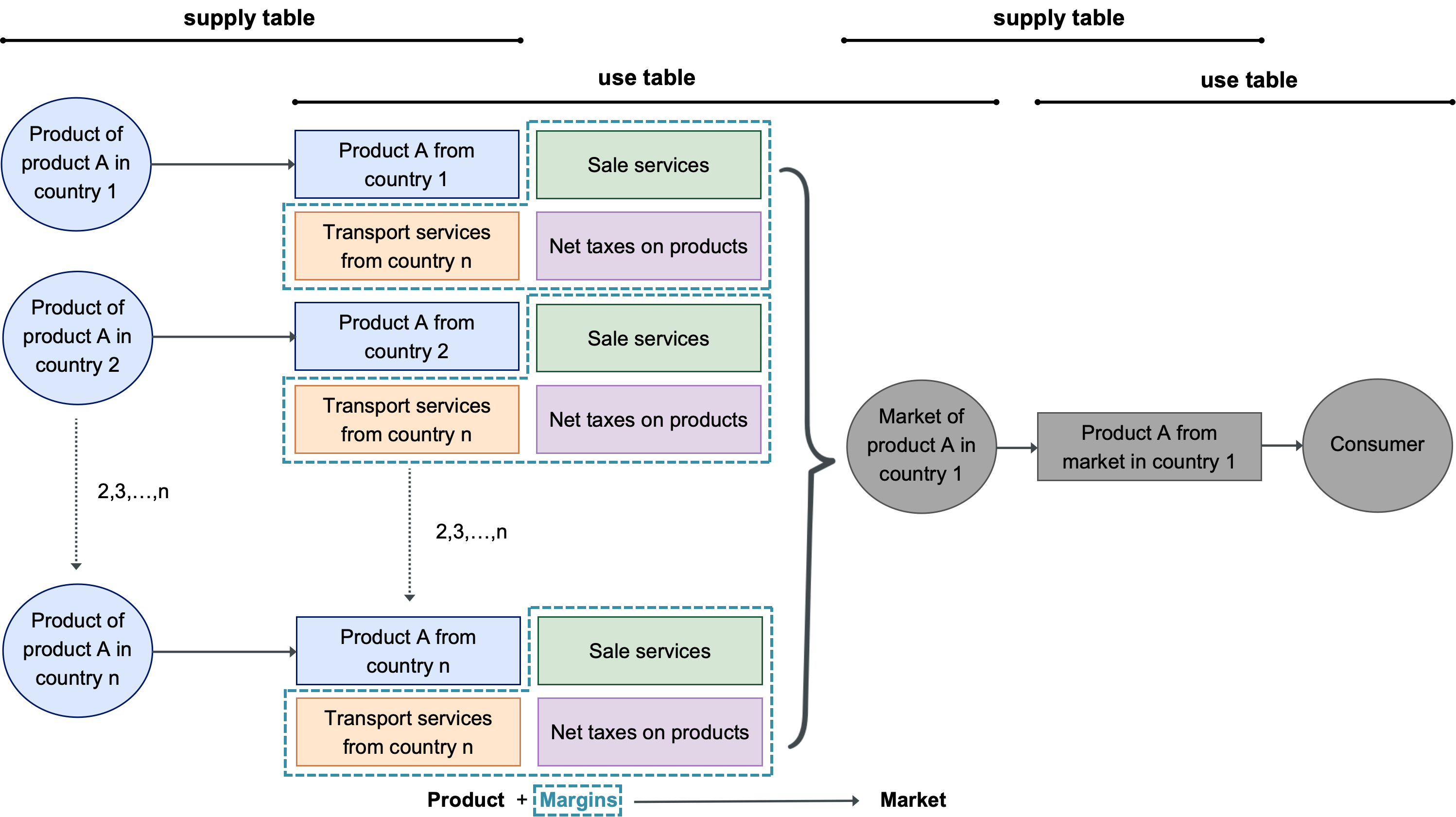
The Markets#
A market is an intermediate activity between producers and users.
Producers from several countries (exporting activities) feed products to a national market (importing country). Other inputs to the markets are:
the transport services to move the products from the origin country to the destination one;
trade services which includes all the other margins of the trade intermediaries;
net taxes on products.
The market is the entity where basic prices are converted into purchaser prices.
The National Mix (in future export market)#
A national mix is inserted anytime a traded product is more disaggregated than its producing activities. One of the example is the fish. Fish can be provided by wild caputure
or by aquaculture. However, trade statistics do not distinguish between sources.
A national mix collects homogeneous products from several sources and produces one unique (mixed) product. The output of the national mix is always associated to the lowest product resolution which can be obtained combining trade accounts and use tables.
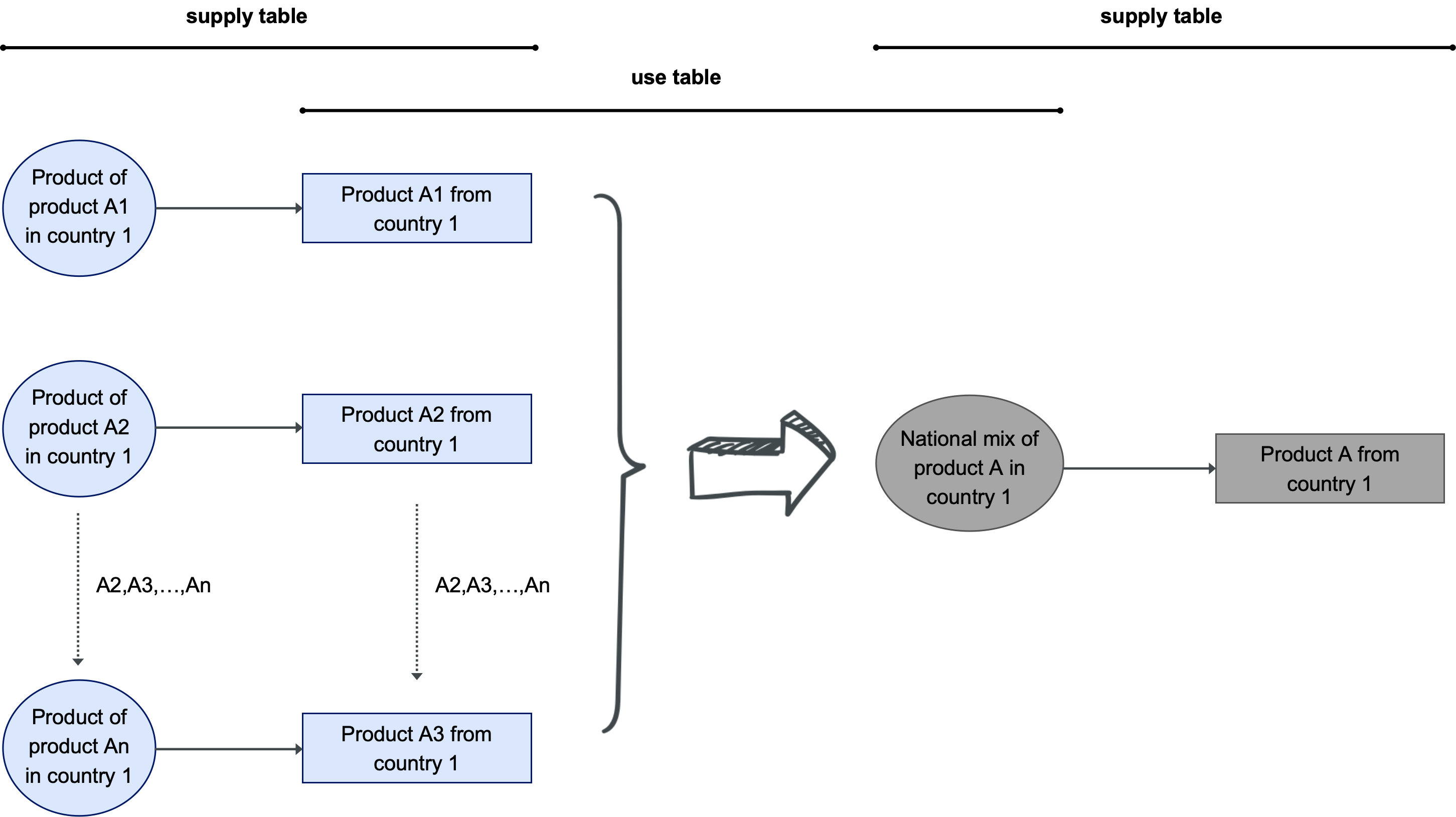
If homogenous products from different producers are not exported from one region to another, there is no need of creating a national mix. Those products will feed to the national markets.
Notice that a national mix differs from conventional market because it does not include trade and sale margins, plus net taxes on products.
Principal Production#
From an economic perspective, the principal production of an activity is the output
from which the highest revenues are gained. The princinpal production is strictly
linked to the sector classification of the activity.
However, in BONSAI IO the choice of the principal production is mostly driven
by the function of the activty rather than the generated economic values.
However, for the majority of cases, both createrias converge to the same principal
production. In other cases, as for some waste treatment services, they could differ.
An example is the incineration of waste. Revenues from the sale of electricity
might exceeds those from the management of waste. In BONSAI, an incineration plant
is always associated to the waste treatement sector. Contrarily, following the economic
definition, an incineration plant might be associated to the electricity sector.
We use in BONSAI IO also the term determing production.
Combined and Joint By-production#
Parameterized Production Function (PPF)#
Parameterized production functions are the least elements to build make-use tables. It defines the relationship between input factors and output factors for a production process. PPFs are embedded into the general make-use framework following the procedures described here
Sectoral Modelling#
Agriculture#
Land Use#
Grass land
Arable land
Forest land
The currently using data source for land use (FAOSTAT) includes the following types of forestry land: primary forest, secondary forest, planted forest, and naturally regenerated forest. In the land use module, we re-classify those forest lands into three categories:Unmanaged forest
Extensively managed forest
Intensively managed forest
First, the theoretical maximum area of managed forest is calculated as:
\[ Area_{\text{manage, max}}=\frac{WR}{Y_{\text{min}}} \]where:
\(WR\): is the annual wood removal (\(m^3\)) in a country.
\(Y_{\text{min}}\): is the minimum yield of managed forests in a country (\(m^3/ha*year\)). This is defined as 1 \(m^3/ha*year\) weighted with potential productivity (based on \(NPP0\)).
If \(Area_{\text{manage, max}}\le(Area_{\text{plant}})\)
the area of intensively managed forest \(Area_{\text{int}}=0\),
the area of extensively managed forest \(Area_{\text{ext}}=Area_{\text{manage, max}}\), and
the area of unmanaged forest \(Area_{\text{unmanaged}}=Area_{\text{prim}}+Area_{\text{sec}}+Area_{\text{nat}}\)
If \(Area_{\text{plant}}<Area_{\text{manage, max}}\le(Area_{\text{plant}}+Area_{\text{nat}})\)
the area of intensively managed forest \(Area_{\text{int}}=0\),
the area of extensively managed forest \(Area_{\text{ext}}=Area_{\text{manage, max}}\), and
the area of unmanaged forest \(Area_{\text{unmanaged}}=Area_{\text{prim}}+Area_{\text{sec}}+(Area_{\text{plant}}+Area_{\text{nat}}-Area_{\text{manage,max}})\)
If \(Area_{\text{manage, max}}>(Area_{\text{plant}}+Area_{\text{nat}})\)
Then, the area of intensively managed forest \(Area_{\text{int}}\) is calculated as follows:
\[ Area_{\text{int, max}} = \frac{WR - (Area_{\text{nat}} + Area_{\text{plant}}) \cdot Y_{\text{min}}}{Y_{\text{int}}} \]where:
\(Area_{\text{int,max}}\): is the theoretical max area intensive managed forest (ha*year) in a country.
\(Y_{\text{int}}\): estimated standard yield of intensive managed forests in a country (\(m^3/ha*year\)). This is defined as 4 \(m^3/ha*year\) weighted with potential productivity (based on NPP0).
\(Area_{\text{int}}=min[Area_{\text{int,max}}, (Area_{\text{nat}} + Area_{\text{plant}})]\)
The area of extensively managed forest \(Area_{\text{ext}}=(Area_{\text{nat}} + Area_{\text{plant}})-Area_{\text{int}}\)
The area of unmanaged forest \(Area_{\text{unmanaged}}=Area_{\text{prim}}+Area_{\text{sec}}\)
Energy#
Packaging#
Packaging “means all products made of any materials of any nature to be used for the containment, protection, handling, delivery and presentation of goods, from raw materials to processed goods, from the producer to the user or the consumer” [EEA].
In BONSAI we assume that each packaging has its own capacity, which can be considered as a service. For example a 50cl bottle provides the service of protecting 50cl of a liquid material.
Activities determine the required packaging based on their capacity needs. The volume of packaging is then converted into mass units. Consequently, activities receive a mass flow from packaging producers that equals the mass of the packaging required. In return, activities pay a corresponding monetary flow to the producers.
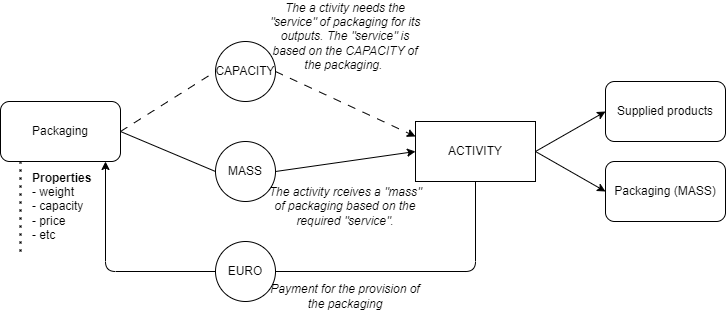
In BONSAI IO packaging supplied by activities to contain their output is reported in the extensions under specific packaging accounts. These packaging accounts describe the use and supply of packaging between suppliers and users. When packaging no longer provides its service, it becomes waste and is subsequently reported in the waste accounts as a regular waste flow.
Trade#
Average Market#
The average market account is calculated using production volume and trade data to estimate domestic market supply for each product. The formula is:
where,
\(V_{\text{market supply}}\): is the total volume of domestic market supply.
\(V_{\text{domestic production}}\): is the total domestic production.
\(V_{\text{import}}\): is the total import.
\(V_{\text{export}}\): is the total export.
It indicates that each product has its own domestic market, where domestic production and import are not differentiated. Additionally, re-exports needs to be identified and adjusted as those goods do not contribute to the domestic market. Re-exports are identified using the following logic:
For locations that import a product from a re-exporting location, its import will be sourcing from the market supply of the re-exporting location instead of the industrial supply.
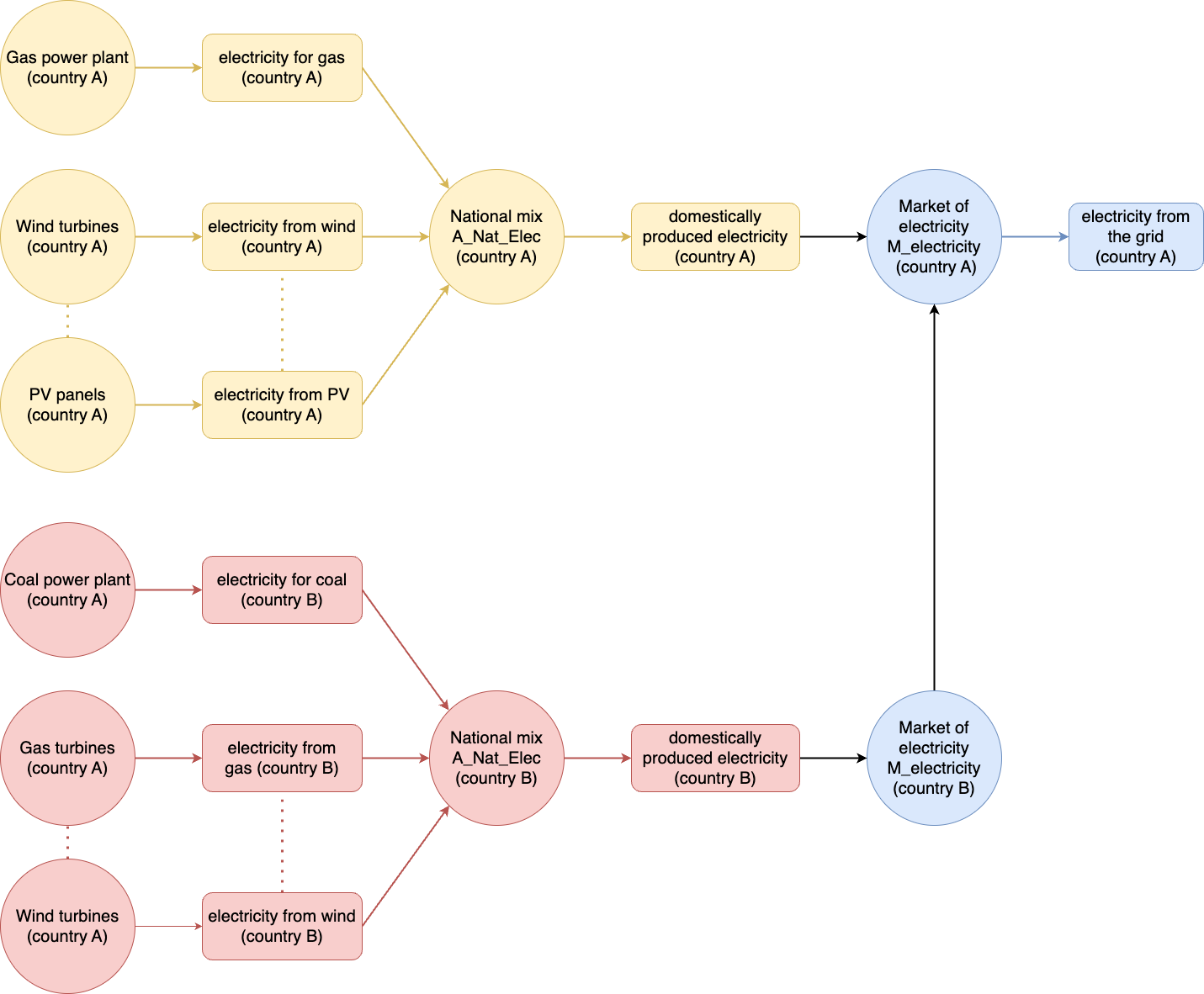
Special treatment is given to the delineation of electricity markets. Electricity market is composed of two market: domestic production (i.e. the national mix) and import markets. The domestic production mix is composed of different domestic electricity generation technologies, e.g., solar PV, wind, and nuclear power. No individual markets are defined for each technology; all are grouped under the domestic production mix. The import market consists of electricity imported from foreign sources.
Transport#
The Transportation module is subdivided into two kinds of transport services: freight transport and passenger transport.
More about the methodology on the construction of the transport account here
Material for Treatment#
A material for treatment is a by-product of activities that needs a further treatment before being able to replace other matherials.
Materials for treatment include waste flows but also scraps that are sold by activities who gain some revenues. Often the terms waste is used in BONSAI to indicate material for treatment.
Waste supply
Waste use
Emissions#
The emission account compiles data on the direct emissions produced by various activities. This account is constructed by combining information from the product supply account and the emission coefficient account. Specifically, it quantifies emissions based on the total supply of principal products and the corresponding emission coefficients for each activity.
The emissions are calculated using the following formula:
\(B\): is the emission matrix that represents direct emissions of activities.
\(E\): is the emission coefficient matrix that represent direct emission coeffient of activities.
\(V_{d}\): is the diagonal entries of the supply matrix.
The emission coefficient account is compiled based on different data sources including bonsai-ipcc,
Properties#
The property account includes the conversion factors to convert a product flow across different property layers. It includes the following conversion factors:
Price
Heat value
Weight
Dry matter content
Balance#
A graph-based multi-layer SUT balance framework is developed to balance the hybrid supply and use tables, as shown in the figure below:
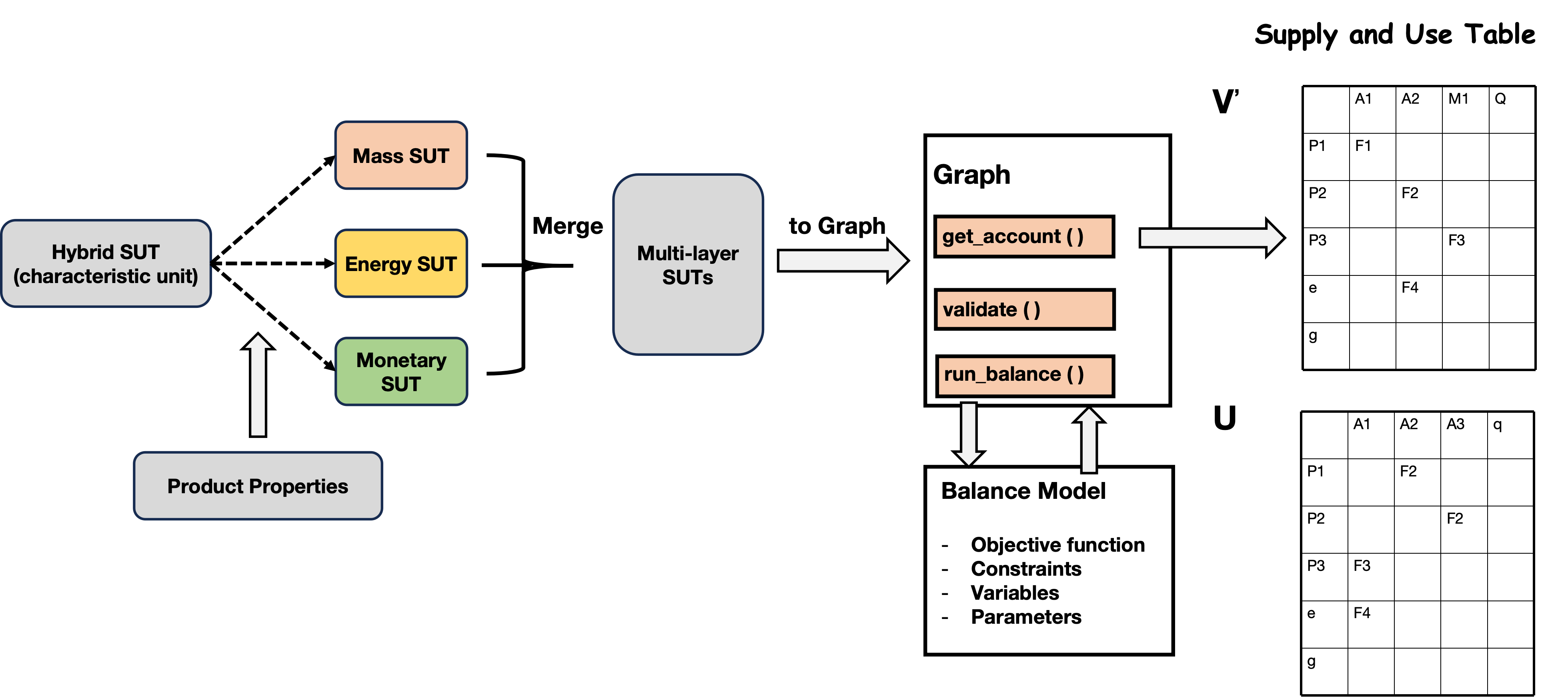
The balance problem is formulated as follows:
where:
\(\alpha_{ijk}\): Adjustment factor for supply of product \(i\), activity \(j\), and unit \(k\).
\(\beta_{ijk}\): Adjustment factor for use of product \(i\), activity \(j\), and unit \(k\).
\(v_{ijk}\): Initial supply volume of product \(i\) by activity \(j\) in unit \(k\).
\(v_{ibk}\): Initial supply volume of the base/determining product \(b\) by activity \(j\) in unit \(k\).
\(u_{ijk}\): Initial use volume of product \(i\) by activity \(j\) in unit \(k\).
\(P_j\): Set of products co-produced by activity \(j\).
\(r_{p, j}\): The initial ratio between products \(p\) and \(b\) by activity \(j\) (\(v_{pjk}/v_{bjk}\)).
Constraints
Product Balance ensures total supply of a product equals its total use.
Activity Balance ensures total input to an activity does not exceed its total output.
Output Ratio Constraint ensures the ratio of co-produced products for an activity remains constant.
Flow balance
To be added
Activity balance
It is imposed that for each inputs to an activity the following condition holds:

Disaggregation#
Household
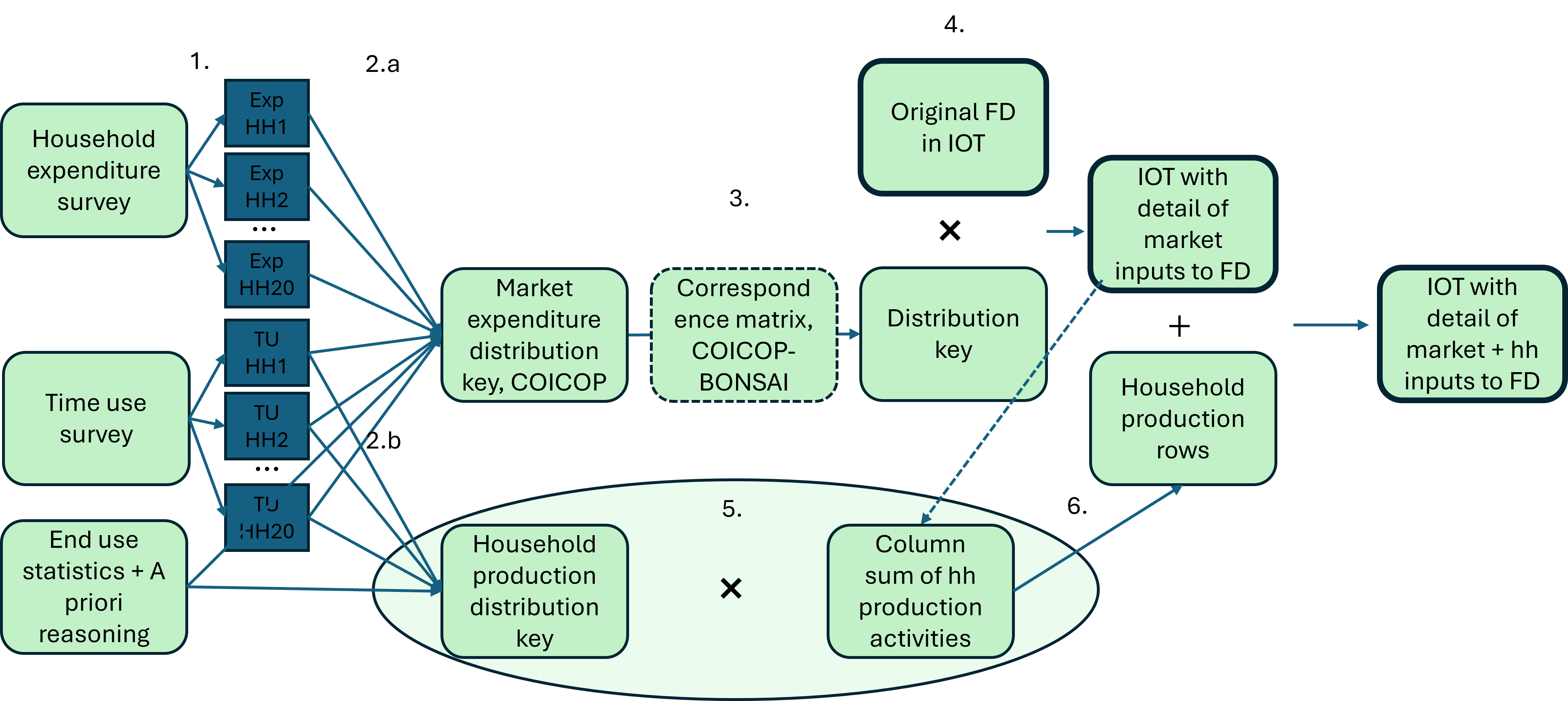
The household production and consumption are disaggregated via distribution keys generated by household expenditure and time-use survey following the formula below.
For the use matrix:
where:
\(U_{f}\): is disaggregated use matrix by household, with dimensions \(p \times a\).
\(D_{use}\): is the market use distribution key matrix of size \(p \times a\), containing non-negative elements no greater than 1. A market use distribution key \(d_{p,a}\) shows the percentage of each product used per household group-activity with each summing to 1
\(f\): is the household final demand vector of dimensions \(p \times 1\).
For the supply matrix:
where:
\(V_{w}\): is disaggregated household supply matrix, with dimensions \(a \times p\).
\(D_{supply}\): is the product supply distribution key matrix of size \(p \times a\), containing non-negative elements no greater than 1. A market use distribution key \(d_{p,a}\) shows the percentage of each product used per household group-activity with each summing to 1
\(f\): is the labor supply vector of dimensions \(p \times 1\).
The full workflow to disaggregate the houshold production and consumption is as follows:
<<<<<<< HEAD#
2. Consequential Modelling#
dev
2. Transformation into Input-Output tables#
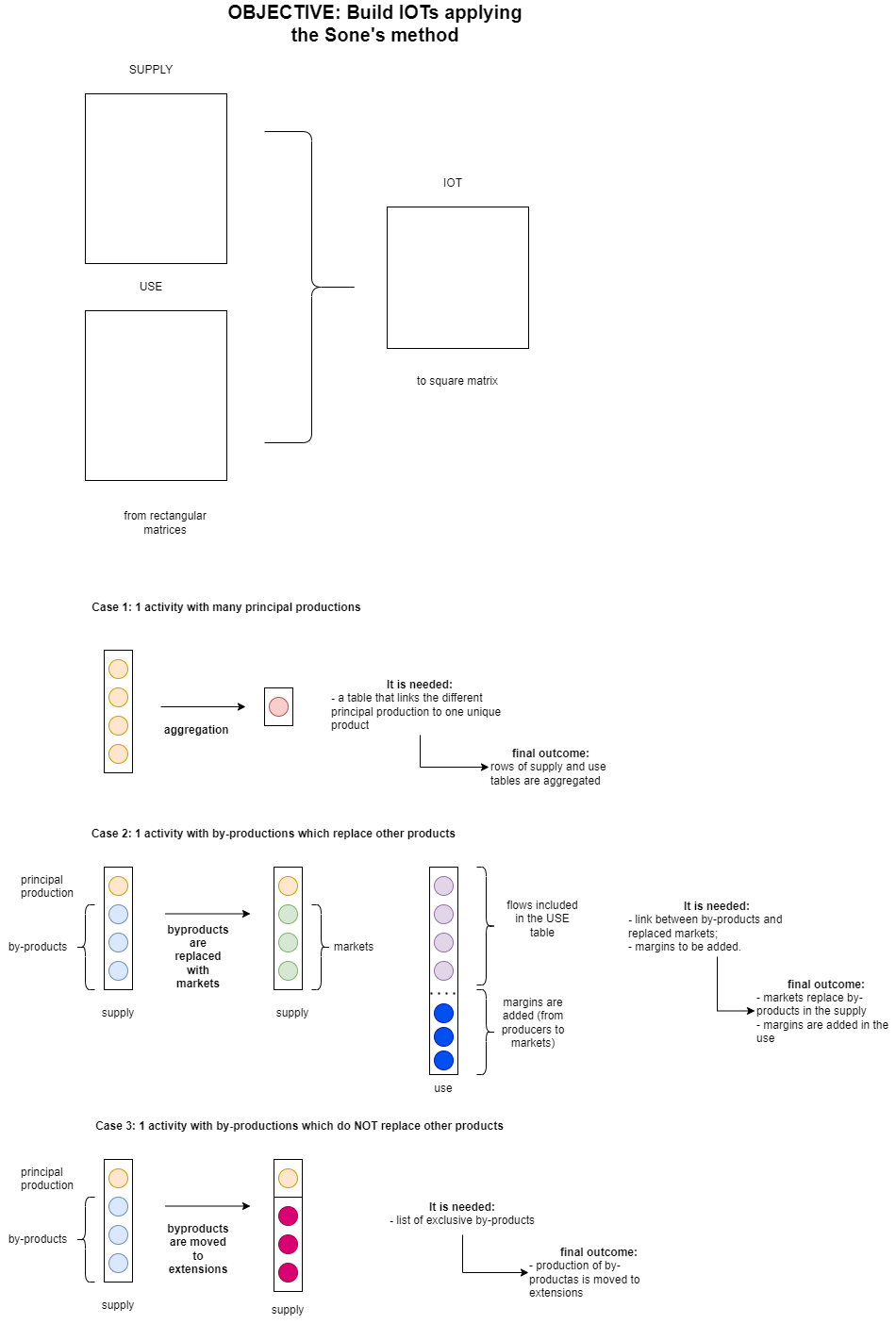
The compiled make-use system is only a mirror of the past biosphere-technosphere interactions, to serve the accounting purpose. Therefore, it only serves as a descriptive tool.
If the aim is to estimate the footprints of products or processes, some assumptions must be adopted. Therefore, we move from an accounting tool to a modeling one.
In practice, this process consists of linking users and producers of products. This apparently simple transformation is purely subjective and there is a long literature on how to proceed.
There are three main approaches to tranform make-use into input-output tables:
By-product technology model (Stone’s method)
Product technology assumption
Industry technology assumption
Here we have decided to implement the by-product technology model. This approach, developed within the Input-output community, has been adopted by the consequential LCA practioners because it better models the casual-effect link associated with behaviorial changes. Within LCA community, the Stone’s method is defined as system expansions.
By-product Technology Modelling#
The formula is given as:
where:
\(m\): is the environmental intervention, meaning the total of direct and indirect environmental impact, of a product of interest.
\(B\): is the direct emissions of activities.
\(V_{d}\): is the diagonal entries of the supply matrix.
\(V_{od}\): is the off-diagonal entries of the supply matrix.
\(U\): is the use matrix.
\(k\): is a vector of products, in which all entries are zero, except the entry for the product of interest.
3. Consequential modelling#
The compiled make-use system is only a mirror of the past biosphere-technosphere interactions, to serve the accounting purpose. Consequential modellun aims to model the casual-effect link associated with behaviorial changes, i.e., how a marginal change in demand affect upstream supply. The system is then transformed and extended for causal-effect linking, following the consequantial modelling requirements in the ISO 14040 and 14044.
The steps to move from the accounting system to the consequential system includes the following steps:
Byproduct technology model as defined above
Marginal producers
Indirect land use change model
Marginal electricity model
Capital endogenization model
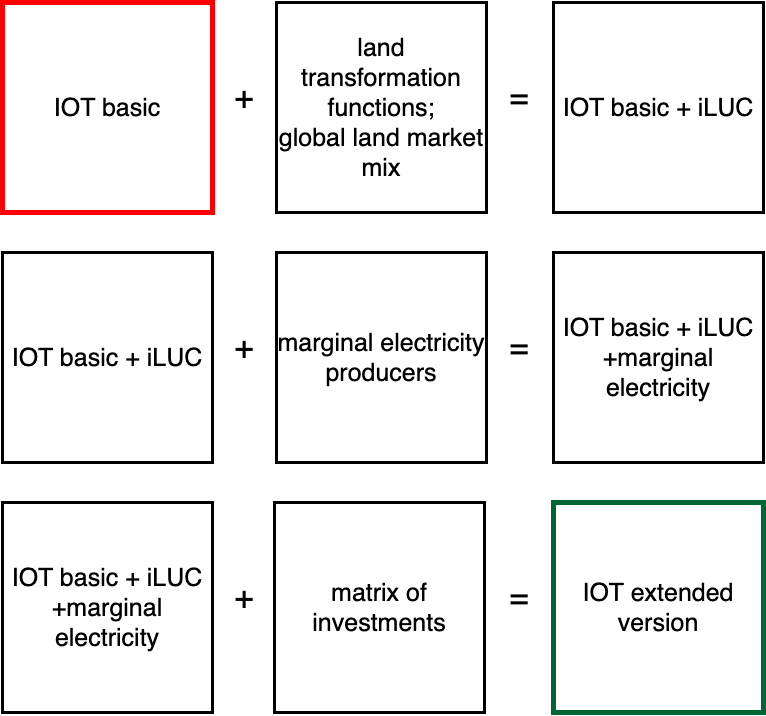
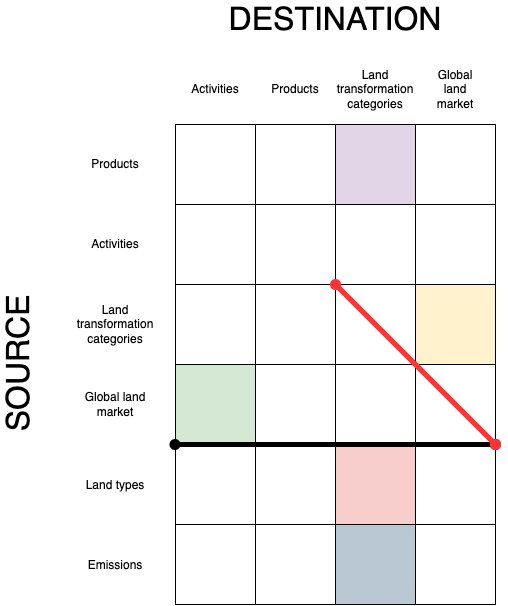
Indirect land use change#
Marginal Electricity Mix#
The formula to calculate the direct requirement matrix \(A\) considering the marginal electricity mix is given by:
where:
\(A\): is the direct requirement matrix.
\(V\): is the supply table.
\(V_{base, elec}\): is the base electricity supply matrix, representing the initial state of electricity supply.
\(\Delta{V_{elec}}\): is the marginal electricity supply matrix.
\(U\): is the use matrix.
The marginal electricity supply is calculated following the logic as follows:
\(V_{\text{elec, base}}\): Base electricity supply matrix, as defined above.
\(M_{\text{elec}}\): Marginal electricity supply matrix, representing the marginal increase in supply of different electricity supply activities responding to the unit increase in electricity demand.
\(\circ\): Denotes element-wise (Hadamard) multiplication.
The marginal electricity supply matrix is then calculated as:
where:
\(v_{j, \text{base}}\): Base value of the electricity supply activity \(j\)
\(v_{j, \text{fture}}\): Future value of the electricity supply activity \(j\)
\(t_{base}\): Initial time period.
\(t_{future}\): Future time period.
\(\delta\): The capital replacement rate/deprecation rate below which the marginal increase is considered negligible and thus set to zero.
The future electricity supply is extrapolated based on a net-zero for 2050 scenario from the Global Change Assessment Model (GCAM v6.0) in the NFGS version 4.0 scenario dataset. The scenario assumes that all pledged targets by countries globally to UNFCCC, even if not yet backed up by implemented effective policies. For detailed assumptions and methodology, refer to the documentation.
Capital Endogenization#
The flow matrix approach is applied to endogenize capital goods for footprint assessment. Specifically, the requirement of capital goods by current intermediate activities is added into the requirement matrix using the following formula:
where
\(A\): is the direct requirement matrix.
\(V_{d}\): is diagonal entries of the supply matrix.
\(V_{od}\): is off-diagonal entries of the supply matrix.
\(U\): is the use matrix.
\(U_{C}\): is the capital use matrix, which represents the use of capital goods by current intermediate activities.
The capital use matrix \(U_{C}\) captures the inputs of capital goods in the production of current intermediate activities. It can be calculated from gross fixed capital formation (GFCF) by different capital goods and total consumption of fixed capital (CFC) by current intermediate activities. First, the capital use matrix is derived from the matrix multiplication of the capital requirement matrix and the diagonization of GFCF vector:
where
\(K\): is the capital requirement matrix where its element \(k_{ij}\) represents the share of a capital goods required by an industrial activity. The row sum of the capital requirement matrix shall be either one (has capital goods used by the activity) or zero (no capital goods used by the activity).
\(\hat{GFCF}\): is the diagonalization of the GFCF vector.
The capital requirement matrix is calculated based on consumption of fixed capital as follows:
where
\(I\): is a virtual investment matrix recording the use of capital goods/investment by current intermediate activities.
\(d\): is the vector of total consumption of fixed capital by current intermediate activities.
\(e\): is the summation vector in proper dimensions.
3. Glossary#
Core Concepts for the Make-use Framework#
Activity: Doing or making something.
Product: Output of an activity with a positive market or non-market value (utility).
National mixes: A national mix is inserted anytime a traded prodcut is more disaggregated than its producing activities.
Markets of products: These are aggregate representations of similar products from various producers (e.g., steel from multiple manufacturers), pooled into a market to reflect the typical product mix available for use. They account for average properties, emissions, or energy use across producers.
Markets of processed heat/fuels: These are specific types of product markets focused on thermal energy or fuel types (e.g., district heat, diesel, biogas), reflecting aggregated supply from multiple production routes or regions. These markets smooth over differences in source inputs to provide an average supply characteristic.
Combustion processes: These represent specific technological activities where fuels are burned to produce energy, heat, or mechanical work — and are a major source of emissions inventories (e.g., industrial boilers, residential stoves, or vehicle engines). Each combustion process typically has a distinct emissions profile depending on fuel type and technology.
Markets of waste treatments: These are modeled entities representing how different waste streams (e.g., municipal solid waste, hazardous waste, sewage sludge) are typically treated — via incineration, landfilling, recycling, composting, etc. They can represent national average treatment pathways for specific waste types.
Packaging materials: Materials used to protect or contain products (e.g., plastic film, cardboard, glass bottles). They are modeled as separate product flows because they have distinct life cycles and disposal routes and significantly influence waste generation and recycling rates.
Emissions: These are residual flows from processes to the environment (the biosphere). Emissions include CO₂, NOₓ, particulate matter, heavy metals, etc., and are typically tracked in physical units (e.g., kg/year). They are crucial for assessing environmental impacts.
Waste (products) flows to be collected: These are post-consumer flows of products that become waste and are collected by waste management systems. This includes recyclable materials, organic waste, or non-recyclables — typically in mixed or sorted streams.
Waste fractions flows to be treated: After collection, waste is sorted into fractions (e.g., plastic, glass, organics) and sent to treatment processes (e.g., mechanical sorting, pyrolysis, composting). These flows represent the routing of specific waste types to their respective treatment technologies.
Stocks: Physical quantities of materials or products that are accumulated in the economy but not immediately consumed or disposed. This includes construction materials in buildings, cars in use, electronics in households, etc. Stocks influence future waste generation and resource demand.
Value added: This is the economic contribution of a production activity — typically measured as output minus intermediate consumption. It includes wages, profits, and taxes, and is crucial in linking physical flows with monetary input-output models.
Other residuals in natural unit: These include non-emission, non-waste residual flows, such as heat losses, rejected water, noise, or byproducts in physical terms (e.g., MJ, liters, kg) that don’t fit into conventional product or emission categories but are still environmentally relevant.
